Learn about Parabola

The intersection of the surface of a cone with a plane results in a conic section. The mathematician, Apollonius of Perga, gave the conic sections their names. As far as the JEE Main exam is concerned, the conic section is a topic of great importance. Students can easily score from this topic if they learn thoroughly. They can expect 2 questions from this topic for any entrance exam. We can draw the graph of a conic section on a coordinate plane. A conic section has some features like one focus, eccentricity, directrix, etc. 

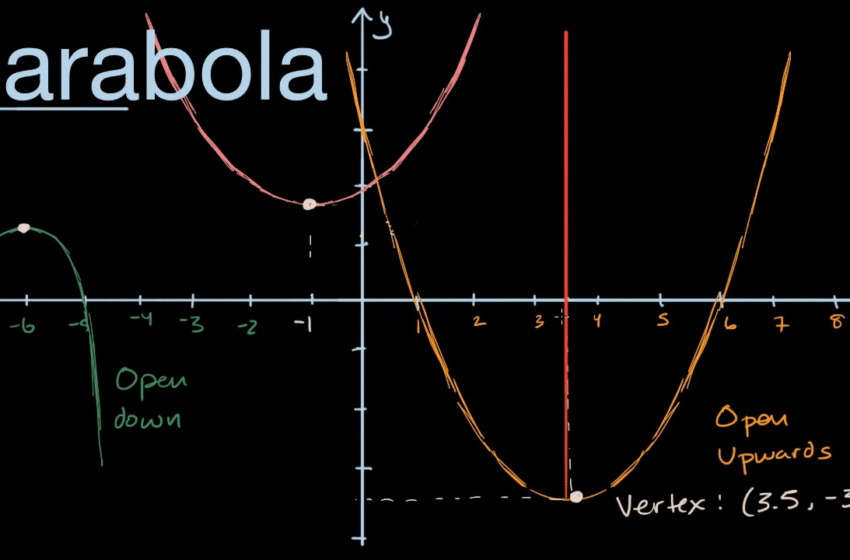
In the Euclidean plane, conic sections have various properties, many of which can be used as alternative definitions. The value of the eccentricity determines the type of conic. In analytic geometry, a plane algebraic curve of degree 2 defines a conic. There are three types of conic sections. A parabola is a type of conic section obtained when the plane is parallel to the generating line. We can also define it as a U-shaped plane curve where any point is at an equal distance from a fixed point and from a fixed straight line. The fixed point is called the focus, and the fixed line is known as the directrix. Following are some important terms related to the conic section. 

• Vertex
• Locus
• Focus
• Directrix

The vertex is the point halfway between the focus and the directrix. The standard equation of a parabola is y² = 4ax. If it is parallel to the x-axis, then the equation is given by x² = 4ay. The eccentricity is always equal to 1.

Important Formulas 

(1) Length of latus rectum = 4a

(2) The chord of contact of the tangents drawn from a point (x₁, y₁) to y² = 4ax is given by T = 0, i.e. yy₁ – 2a(x + x₁) = 0. 

(3) If (x₁, y₁) is the midpoint, then the equation of the chord of y² = 4ax is T = S₁.

(4) In parametric form, we denote the curve by x = at² and y = 2at.

(5) If (x₁, y₁) is an external point on y² = 4ax, then the pair of tangents is given by SS₁ = T², where S = y²-4ax, T = yy₁-2a(x+x₁) and S₁ = y₁²-4ax₁.

Hyperbola

We can define hyperbola as a type of smooth curve lying in a plane. It has two pieces, known as the branches. These are mirror images of each other. It resembles two infinite bows. It is a type of conic section formed by the intersection of a plane and a double cone. The standard equation is given by x²/a² – y²/b² = 1. The eccentricity is greater than 1. The eccentricity gives an idea of the ovalness of the conic.

Students are recommended to learn the important formulas of the conic section. PDFs of chapter-wise questions and previous years’ solved question papers are available online. Students should make use of these resources and prepare for the JEE Main and the JEE Advanced exam. This will help to boost problem-solving skills. Through proper planning and hard work, one can easily crack the JEE exams.